Neural Flight: Model Predictive controller for Bi-copter
Gradient-based Algorithms and Differentiable Programming
1. Introduction
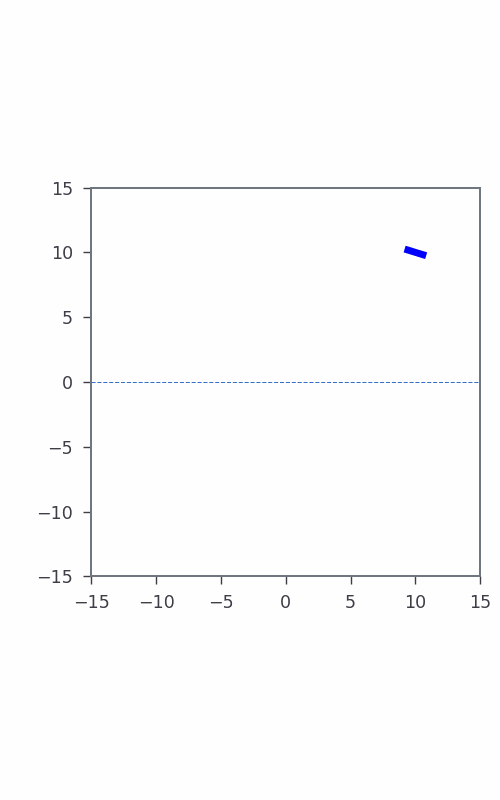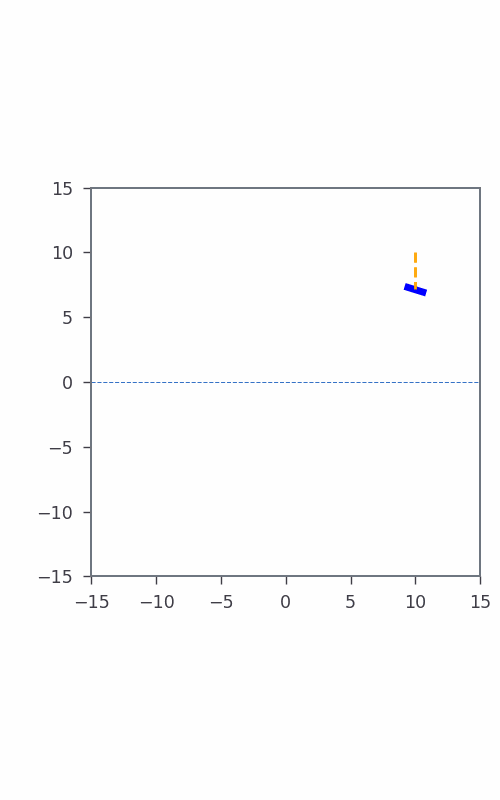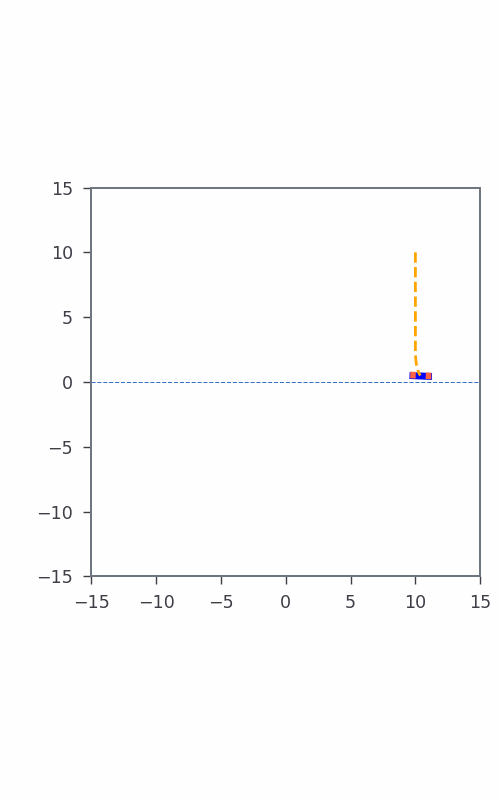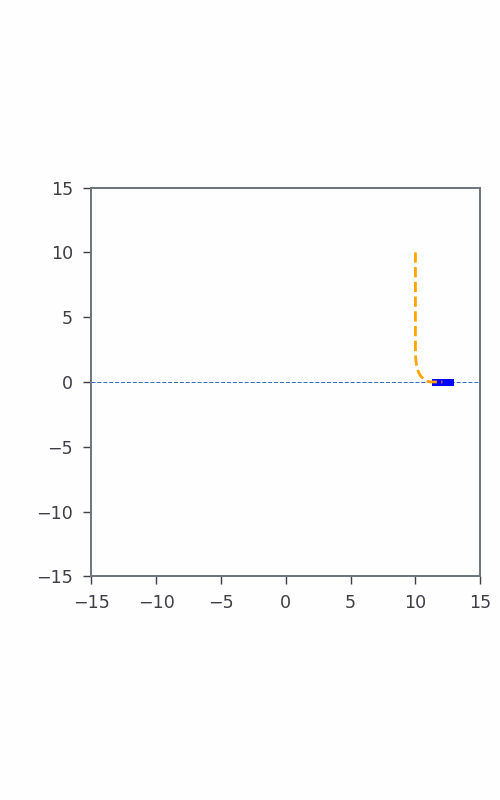
Consider a simple formulation of Bicopter hovering at a point in space where the dynamic state vector $\textbf{x}(t)$ is represented by its coordinates $y(t)$, $z(t)$, and $\theta(t)$ velocity $\dot{y}(t)$, $\dot{z}(t)$, and $\dot{\theta}(t)$, i.e., $\textbf{x}(t) = [y(t), z(t), \theta(t), \dot{y}(t), \dot{z}(t), \dot{\theta}(t)]^T$, where $t$ specifies time. The control input $\textbf{u}(t)$ to Bicopter includes thrust $u_1(t)$ and $u_2(t)$. The discrete-time dynamics follows
\[\begin{aligned} & y(t+1) = y(t) + \dot{y}(t) \Delta t + 0.5 (\frac{u_1(t) + u_2(t)}{m})\sin(\theta(t)) \Delta t^2, \\ & z(t+1) = z(t) + \dot{z}(t) \Delta t + 0.5 (\frac{u_1(t) + u_2(t)}{m})\cos(\theta(t)) \Delta t^2, \\ & \theta(t+1) = \theta(t) + \dot{\theta}(t) \Delta t + 0.5 (\frac{(u_1(t) - u_2(t))*L}{I_{xx}})\Delta t^2, \\ \\ & \dot{y}(t+1) = \dot{y}(t) + (\frac{u_1(t) + u_2(t)}{m})\sin(\theta(t)) \Delta t \\ & \dot{z}(t+1) = \dot{z}(t) + (\frac{u_1(t) + u_2(t)}{m})\cos(\theta(t)) \Delta t \\ & \dot{\theta}(t+1) = \dot{\theta}(t) + (\frac{(u_1(t) - u_2(t))*L}{I_{xx}}) \Delta t, & \end{aligned}\]where $\Delta t$ is a time interval. Further, let the closed-loop controller be
\[\textbf{u}(t) = [u_1(t), u_2(t)] = \pi_{w}(\textbf{x}(t))\]where $\pi_{w}(\cdot)$ is a neural network with parameters $w$, which are to be determined through optimization.
| For each time step, we assign a loss as a function of the control input and the state: $l(\textbf{x}(t),\textbf{u}(t))$. In this example, we will simply set $l(\textbf{x}(t),\textbf{u}(t))=0$ for all $t=1,…,T-1$, where $T$ is the final time step, and $l(\textbf{x}(T),\textbf{u}(T)) = | \textbf{x}(T) | ^2$. |
The optimization problem is now formulated as
\[\begin{aligned} \min_{w} \quad & \quad ||x(T)||^2 \\ \quad & \quad y(t+1) = y(t) + \dot{y}(t) \Delta t + 0.5 (\frac{u_1(t) + u_2(t)}{m})\sin(\theta(t)) \Delta t^2, \\ \quad & \quad z(t+1) = z(t) + \dot{z}(t) \Delta t + 0.5 (\frac{u_1(t) + u_2(t)}{m}\cos\theta(t)- g) \Delta t^2, \\ \quad & \quad \theta(t+1) = \theta(t) + \dot{\theta}(t) \Delta t + 0.5 (\frac{(u_1(t) - u_2(t))*L}{I_{xx}})\Delta t^2, \\ \\ \quad & \quad \dot{y}(t+1) = \dot{y}(t) + (\frac{u_1(t) + u_2(t)}{m})\sin(\theta(t)) \Delta t \\ \quad & \quad \dot{z}(t+1) = \dot{z}(t) + (\frac{u_1(t) + u_2(t)}{m}\cos\theta(t) - g) \Delta t \\ \quad & \quad \dot{\theta}(t+1) = \dot{\theta}(t) + (\frac{(u_1(t) - u_2(t))*L}{I_{xx}}) \Delta t, \\ \quad & \quad \text{u}(t) = \pi_{w}(\textbf{x}(t)), ~\forall t=1,...,T-1 \end{aligned}\]While this problem is constrained, it is easy to see that the objective function can be expressed as a function of $\textbf{x}(T-1)$ and $\textbf{u}(T-1)$, where $\textbf{x}(T-1)$ as a function of $\textbf{x}(T-2)$ and $\textbf{u}(T-2)$, and so on. Thus it is essentially an unconstrained problem with respect to $w$.
In the following, we code the forward pass of the loss using PyTorch, which then automatically computes the gradient $\nabla_{w} l(\textbf{x}(T),\textbf{u}(T))$.
